A continuación veremos los sistemas de numeración mas característicos de la historia, reconociendo los símbolos y los elementos que ellos utilizaron para representar las cantidades.
Numeración romana:
Se basa en el valor absoluto y posición relativa de siete símbolos representados por letras del alfabeto.
Reglas y ejemplos:
Este sistema se basaba en la suma de los símbolos, colocados de tal forma que el de menor valor iría delante del valor mayor.
Ejemplo:
2151 se escribiría MMCLI
1809 se escribiría MDCCCIXCuando a la derecha de una cifra se escribe otra igual o menor, el valor resultante es la suma de los dos valores de las cifras.
Ejemplo:
XX = 20
LXVI = 66
VII = 7
La cifra I colocada a la izquierda de la V o la X, les resta una unidad. A la derecha, les suma una unidad. La cifra X colocada a la izquierda de la L o la C, les resta diez unidades y a la derecha les suma diez unidades. La C colocada a la izquierda de la D o la M, les resta cien unidades y si esta colocada a la derecha les suma cien unidades.
Ejemplo:
IV = 4 XL = 40
IX = 9 CX = 110
Una cifra no se puede repetir más de tres veces seguidas.
Ejemplo:
XIII = 14
XXXIII = 33
XXIV = 24
Las cifras V, L y D no se pueden duplicar ya que la X, C y M representan sus valores duplicados.
Ejemplo:
X representa 10 en lugar de VV
C equivale 100 en lugar de LL
M equivale 1000 en lugar de DD
El valores de los números romanos se multiplica por mil tantas veces como rayas horizontales colocadas encima de estos últimos.
Sistema de numeración egipcia:
Los egipcios usaron un sistema de escribir los números en base diez, utilizando los jeroglíficos de la figura para representar los distintos ordenes de unidades.
Las reglas para representar una cantidad en este sistema son:
a) Cada símbolo puede repetirse hasta nueve veces.
b) Si un símbolo debe escribirse más de cuatro veces, entonces no debe escribirse en una sola línea sino en dos o más renglones.
Por ejemplo:
- Para representar 1 214, separa el número en sus unidades y en grupos de 10 en 10 (decenas, centenas, unidades de millar, etc.). Es decir:
1 214 = 1 000 + 100 + 100 + 10 + 1 + 1 + 1 + 1
Numeración babilónica:
Los números se representaban con la ayuda de solo dos símbolos, una cuña vertical que representaba a la unidad, y una cuña horizontal para el numero diez.
Estas cuñas resaltaban en las tablillas de arcilla, por los palitos inclinados y tomaban la forma de un prisma.
con la ayuda de los dos signos mencionados todos los numeros enteros del 1 al 59 se podian escribir exactamente , es decir que los signos para el diez y la unidad se repetian correspondientemente tantas veces fuera nacesario.Hasta aqui no hay ningun problema lo nuevo comienza con la escritura del numero 60, donde se utiliza el mismo signo que para el 1, pero con mayor intervalo entre el y los signos restantes.
En el sistema decimal babilonio, las reglas para representar una cantidad son las siguientes:
- La cuña con valor 1 se podía repetir hasta un total de nueve veces.
- Cuando se repiten símbolos se suman sus valores. A la izquierda se escriben los símbolos mayores.
- Para representar órdenes superiores a 100 se usaba la multiplicación por 10, escribiendo separada una cuña de este valor, a la izquierda de la cantidad multiplicada.
Sin embargo, estas combinaciones no se usaban con mucha frecuencia. Con el paso de los años y con el progreso, los babilonios usaron el sistema sexagesimal (de base sesenta).
Los números menores de sesenta se escribían en el sistema decimal. Los números mayores de sesenta se escribían anotando las cuñas 1 o 10 en distintos lugares a la izquierda. Cada lugar a la izquierda representaba una potencia distinta de 60. Las cuñas indicaban cuántas veces debían multiplicarse cada potencia de 60.
Numeración decimal:
La numeración decimal incorpora una serie de reglas que permiten representar una serie infinita de números.
sus principales características son :su sistema en base 10.
Esto quiere decir que el agrupamiento de este sistema es diez,en donde cada diez unidades forma otro carácter superior, la cual se escribe ala izquierda de la primera de las unidades.
En el sistema decimal el número 528, por ejemplo, significa:
5 centenas + 2 decenas + 8 unidades, es decir:
5*102 + 2*101 + 8*100 o, lo que es lo mismo:
500 + 20 + 8 = 528
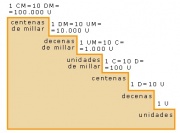
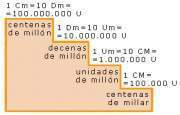
Para números más grandes con más de seis cifras, hemos de usar órdenes de unidades superiores a la centena de millar:
Entonces:
Si la unidad se divide en 10 partes iguales, cada una de ellas es una décima; si se divide en 100 partes iguales, se obtienencentésimas. Y, si seguimos, aparecenmilésimas, diezmilésimas, cienmilésimas,millonésimas...
Una centena tiene 10 decenas, cada decena tiene 10 unidades, cada unidad tiene 10 décimas, cada décima tiene 10 centésimas, cada centésima tiene 10 milésimas.
A la izquierda de la coma decimal esta la parte entera y ala derecha la parte decimal.
Se llama sistema decimal o de base 10, porque 10 unidades de un orden cualquiera forman 1 unidad del orden inmediato superior
Es un sistema posicional porque el valor de una cifra depende de la posición que ocupe dentro del número que estemos considerando.
Los seis primeros órdenes de unidades son:
- Centenas de Millar (CM)
- Decenas de Millar (DM)
- Unidades de Millar (UM)
- Centenas (C)
- Decenas (D)
- Unidades (U)
- Centenas de Millón (Cm)
- Decenas de Millón (Dm)
- Unidades de Millón (Um)
- Centenas de Millar(CM)
Numeración binaria:
El sistema de numeración binario u un sistema de posición donde cada dígito binario(bit) y tiene un valor basado en su posición relativa al LSB.Cualquier numero binario puede convertirse en su equivalente decimal,simplemente sumando en el numero binario las diversas posiciones que contengan un 1.
por ejemplo:
1 1 1 0 1 12 de binario a decimal
1 x 25 + 1 x 24 + 1 x 23 + 0 x 22 + 1 x 2 + 1 = 6910
1 x 25 + 1 x 24 + 1 x 23 + 0 x 22 + 1 x 2 + 1 = 6910
Procedimiento para convertir un numero de decimal a binario.
Ejemplo:
Se divide el número del sistema decimal entre 2, cuyo resultado entero se vuelve a dividir entre 2, y así sucesivamente hasta que el dividendo sea menor que el divisor, 2. Es decir, cuando el número a dividir sea 1 finaliza la división.
A continuación se ordenan los restos empezando desde el último al primero, simplemente se colocan en orden inverso a como aparecen en la división, se les da la vuelta. Éste será el número binario que buscamos.
A continuación se ordenan los restos empezando desde el último al primero, simplemente se colocan en orden inverso a como aparecen en la división, se les da la vuelta. Éste será el número binario que buscamos.
- Transformar el número decimal 131 en binario. El método es muy simple:
131 dividido entre 2 da 65 y el resto es igual a 1
65 dividido entre 2 da 32 y el resto es igual a 1
32 dividido entre 2 da 16 y el resto es igual a 0
16 dividido entre 2 da 8 y el resto es igual a 0
8 dividido entre 2 da 4 y el resto es igual a 0
4 dividido entre 2 da 2 y el resto es igual a 0
2 dividido entre 2 da 1 y el resto es igual a 0
1 dividido entre 2 da 0 y el resto es igual a 1
-> Ordenamos los restos, del último al primero: 10000011
Numeración octal:
Es también muy usado
en la computación por tener una base que es potencia exacta de 2 o de la
numeración binaria. Esta característica hace que la conversión a binario o
viceversa sea bastante simple. El sistema usa 8 dígitos (0,1,2,3,4,5,6,7) y
tienen el mismo valor que en el sistema de numeración decimal.
Como el sistema
de numeración octal usa la notación posicional entonces para el número 3452.32q tenemos:2*(80) + 5*(81) + 4*(82) + 3*(83) + 3*(8-1) + 2*(8-2) = 2 + 40 + 4*64 +
64 + 3*512 + 3*0.125 + 2*0.015625 = 2 + 40 + 256 + 1536 + 0.375 + 0.03125 =
1834 + 40625,entonces 3452.32q =1834.40625d
Numeración hexagesimal:
—Necesita 16 cifras
y/o letras para poder expresar una cantidad.
—Ver la siguiente
lista: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F.
Por ejemplo: 3E0A16 = 3×163 + E×162 + 0×161 + A×160 = 3×4096 + 14×256 + 0×16 + 10×1 = 15882.




No hay comentarios:
Publicar un comentario